The Complexity of Songs

"The Complexity of Songs" was an article published by Donald Knuth, an example of an in-joke in computer science, namely, in computational complexity theory. The article capitalizes on the tendency of popular songs to evolve from long and content-rich ballads to highly repetitive texts with little or no meaningful content.^[1]

Article summary

Knuth writes, with a grain of truth, that "our ancient ancestors invented the concept of refrain" to reduce the space complexity of songs, which becomes crucial when a large number of songs is to be committed to one's memory. Knuth's Lemma 1 states that if N is the length of a song, then the refrain decreases the song complexity to cN, where c < 1.^[2]

Knuth further demonstrates a way of producing songs with O(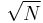) complexity, an approach "further improved by a Scottish farmer named O. MacDonald".^[2]

More ingenious approaches yield songs of complexity O(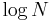), a class known as "m bottles of beer on the wall".

Finally, the progress during the 20th century—stimulated by the fact that "the advent of modern drugs has led to demands for still less memory"—leads to the ultimate improvement: Arbitrarily long songs with space complexity O(1), e.g. for a song to be defined by the recurrence relation^[2]

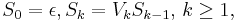
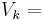'That's the way,' 'I like it,' , for all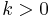

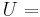'uh huh, uh huh'

Further results

Prof. Kurt Eisemann of San Diego State University in his letter to the Communications of the ACM^[3] further improves the latter seemingly unbeatable estimate. He begins with an observation that for practical applications the value of the "hidden constant" c in the Big Oh notation may be crucial in making the difference between the feasibility and unfeasibility: for example a constant value of 10⁸⁰ would exceed the capacity of any known device. He further notices that a technique has already been known in Mediaeval Europe whereby textual content of an arbitrary tune can be recorded basing on the recurrence relation 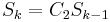, where 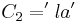, yielding the value of the big-Oh constant c equal to 2. However it turns out that a culture more advanced than the European one achieved the absolute lower bound of O(0)! As Prof. Eisermann puts it:

When the Mayflower voyagers first descended on these shores, the native Americans, proud of their achievement in the theory of information storage and retrieval, at first welcomed the strangers with the complete silence. This was meant to convey their peak achievement in the complexity of songs, namely the demonstration that a limit as low as c=0 is indeed obtainable.

However the Europeans were unprepared to grasp this notion and the Indian chiefs, in order to establish a common ground to convey their achievements later proceeded to demonstrate an approach described by the recurrent relation 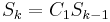, where 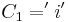, with a suboptimal complexity given by c=1.^[1][3]

References

External links

• "The Complexity of Songs", Knuth, Donald E. (1984).